Fabulous Tips About Can Ohm's Law Be Broken

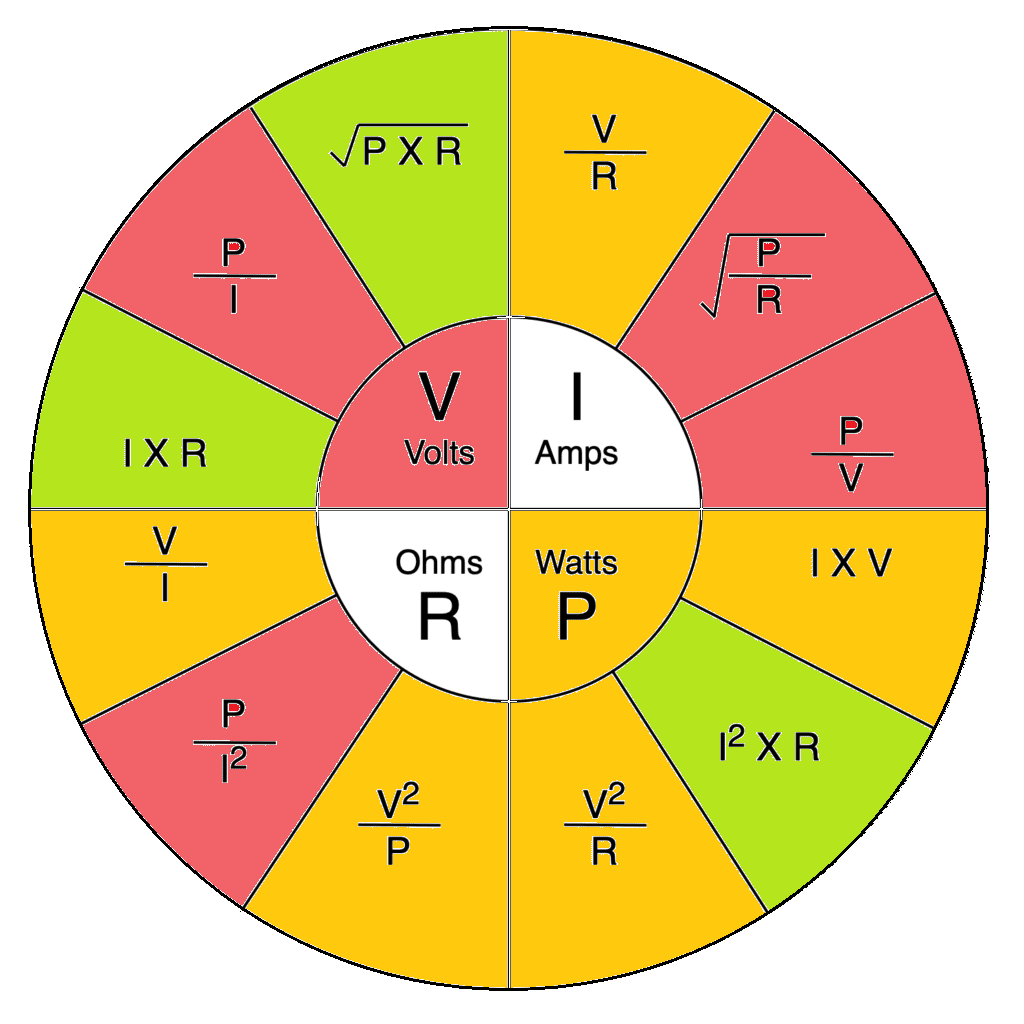
Ohm's Law

1. Understanding the Foundation

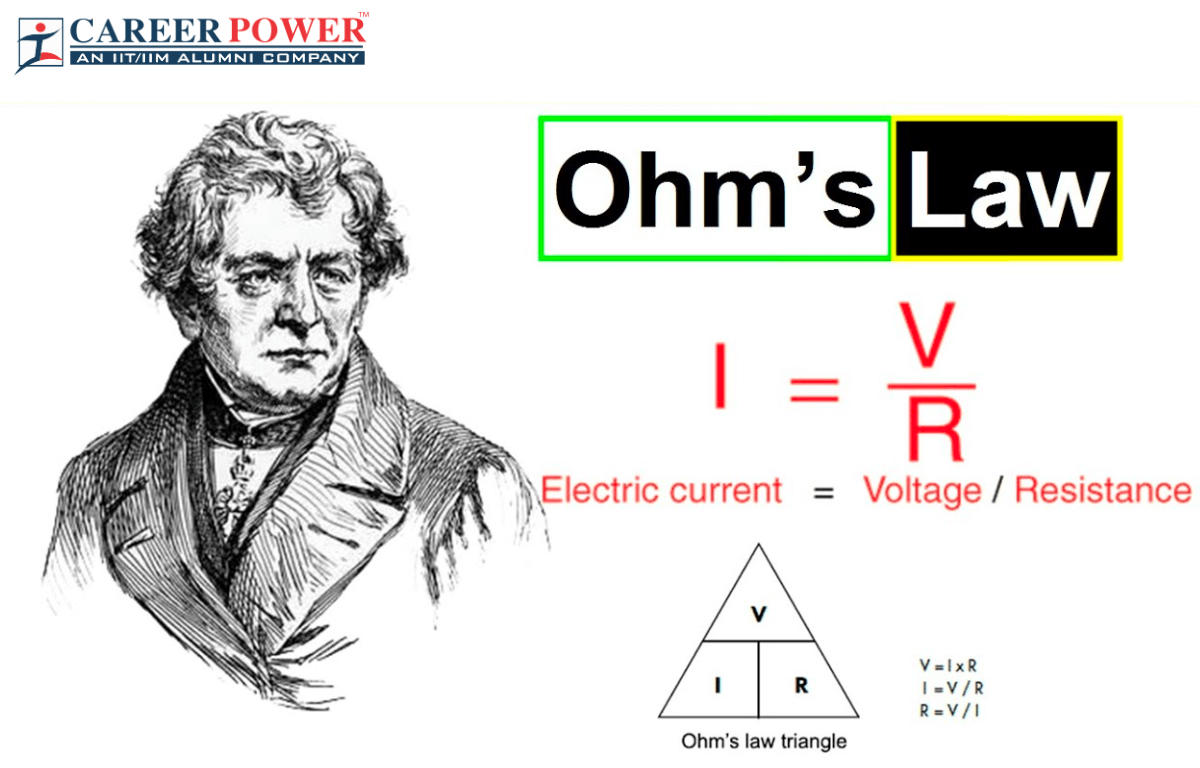
Ohm's Law, the cornerstone of electrical circuit analysis, elegantly states that voltage (V) across a conductor is directly proportional to the current (I) flowing through it, with resistance (R) acting as the proportionality constant. Simple, right? V = IR. We teach it in schools, we use it in countless calculations, and it generally works like a charm. But what happens when it doesn't work? Is Ohm's Law some kind of immutable decree, or can it be bent, perhaps even broken?

The short answer is: it's more of a guideline than a rigid rule. Think of it like this: you can usually predict how long a drive will take based on the distance and your speed. But what about traffic jams, detours, or that sudden craving for the world's best ice cream that adds an hour to your journey? Ohm's Law has its limitations too.

The resistance mentioned in Ohms Law is assumed to be constant. However, many things can affect resistance, like temperature. A light bulb filament, for example, has a vastly different resistance when its cold compared to when its glowing brightly. This change throws a wrench into the equation if you're trying to apply Ohm's Law with unwavering precision.

So, before we get too comfortable declaring Ohm's Law inviolable, let's dig a little deeper. There are several instances where the straightforward relationship begins to wobble. Understanding these scenarios helps us appreciate the law's limitations and when to use more sophisticated techniques.

When Ohm's Law Takes a Vacation

2. Non-Ohmic Materials

One of the biggest culprits in Ohm's Law's apparent "breakage" lies in the type of material we're dealing with. Many materials, particularly semiconductors like diodes and transistors, are decidedly non-ohmic. Their resistance isn't constant; it varies with the voltage or current applied. Imagine trying to predict your ice cream stop if the store mysteriously changes its location every time you get close! That's essentially what's happening with non-ohmic materials.

Diodes, for instance, allow current to flow easily in one direction but block it in the other, quite unlike a resistor that impedes current equally in both directions. Similarly, the behavior of transistors is far more complex, relying on controlling current flow based on the input signal, rather than offering a fixed resistance.

The point is, for these components, you can't simply plug in values into V = IR and expect an accurate result. You need to consider their specific characteristics, often described by complex mathematical models or, more practically, data sheets provided by the manufacturer.

Think of Ohm's Law as a helpful map for a familiar city, and non-ohmic materials as a completely different city with its own unique road system. Your old map just won't cut it! You need specialized tools and understanding to navigate these complexities.

AC Circuits and Impedance

3. The Reactive World

Ohm's Law in its simplest form works beautifully for DC (Direct Current) circuits, where the current flows in one direction only. But when we introduce AC (Alternating Current) circuits, where the current constantly changes direction, things get more interesting. Capacitors and inductors, common components in AC circuits, store energy and oppose changes in voltage and current, respectively. This opposition isn't a simple resistance; it's called impedance.

Impedance (Z) is a complex number that combines resistance (R) and reactance (X), the opposition offered by capacitors and inductors. So, instead of V = IR, we now have V = IZ, where I is also a complex number representing the magnitude and phase of the current. Suddenly, things get a lot more mathematical!

Reactance varies with the frequency of the AC signal. The higher the frequency, the greater the reactance of an inductor, and the lower the reactance of a capacitor. This frequency dependence means that the relationship between voltage and current is no longer a simple straight line, but a more complex curve.

Trying to apply the standard Ohms Law to an AC circuit with reactive components is like trying to measure the length of a wriggling worm with a ruler you'll get a number, but it won't be particularly useful. You need to understand impedance and phase relationships to accurately analyze AC circuits.

Temperature's Role

4. Resistance is Relative

We touched upon this earlier, but it's worth emphasizing: temperature has a significant influence on resistance. Most materials exhibit a change in resistance as temperature fluctuates. In metals, resistance generally increases with temperature, while in semiconductors, it typically decreases. Think of it like this: at higher temperatures, the atoms in a metal vibrate more vigorously, hindering the flow of electrons and thus increasing resistance.

This temperature dependency is a critical factor in many applications. For example, thermistors are temperature-sensitive resistors used in temperature sensing circuits. Their resistance changes predictably with temperature, allowing them to be used as accurate temperature sensors.

So, if you're performing measurements and calculations using Ohm's Law, remember to consider the temperature. Ignoring it can lead to significant errors, especially in sensitive circuits or extreme environments.

Imagine trying to bake a cake without knowing the oven's temperature. You might get something edible, but it's unlikely to be perfect. Similarly, neglecting temperature effects in electrical circuits can lead to unexpected and undesirable results.

High Voltages and Electric Fields

5. Beyond Linearity

At very high voltages, materials can exhibit non-linear behavior that defies Ohm's Law. The intense electric field can cause ionization of the material, leading to a sudden increase in current. This phenomenon is known as dielectric breakdown and can be destructive. Think of it like forcing too much water through a pipe eventually, the pipe bursts.

Furthermore, at extremely high frequencies, the skin effect becomes significant. This phenomenon causes the current to flow mainly on the surface of the conductor, effectively reducing the cross-sectional area available for conduction and thus increasing the resistance.

These high-voltage and high-frequency effects are often negligible in everyday low-voltage circuits, but they become crucial in high-power applications, such as power transmission lines or high-frequency communication systems.

When dealing with these extreme conditions, you need to move beyond the simple V = IR relationship and consider more complex models that account for these non-linear effects.

FAQ

6. Your Questions Answered

Let's tackle some common questions about Ohm's Law and its limitations.

Q: Is Ohm's Law always accurate?

A: No, Ohm's Law is an approximation that works well for many linear, time-invariant resistive materials at constant temperatures and DC conditions. It starts to lose accuracy with non-ohmic materials, AC circuits containing reactive components, significant temperature variations, and at very high voltages or frequencies.

Q: What are some examples of non-ohmic devices?

A: Diodes, transistors, light bulbs (due to temperature changes in the filament), and many semiconductor devices are examples of non-ohmic devices. Their resistance changes with voltage or current, so Ohm's Law doesn't apply directly.

Q: How do I analyze circuits where Ohm's Law doesn't apply?

A: For non-ohmic devices, you'll often need to refer to their characteristic curves (graphs showing voltage vs. current). For AC circuits with capacitors and inductors, you need to use impedance and consider phase relationships. For high-voltage or high-frequency situations, more advanced models and simulations may be necessary.

Q: Can I use Ohm's Law as a starting point, even if it's not perfect?

A: Absolutely! Ohm's Law provides a valuable foundation for understanding electrical circuits. Even when it doesn't perfectly describe the behavior, it can still give you a reasonable estimate and a good starting point for further analysis. It's a powerful tool to have in your electrical engineering toolbox, just remember to be aware of its limitations.