Sensational Info About What Are The Conditions For Two Planes To Be Parallel

Parallel Planes
1. Understanding the Basics
Ever wondered what it takes for two planes to be, well, parallel? It's not just about them looking like they're running alongside each other in the sky. There's actually some geometrical harmony involved, and trust me, it's way cooler than it sounds. Think of it like this: two perfectly flat surfaces that are forever destined to never, ever intersect. Like two shy people at a party, always nearby, but never quite connecting. What's the secret sauce?
The key thing to grasp is that parallel planes maintain a constant distance from each other. Imagine two sheets of perfectly flat paper held apart by some invisible force. No matter how far you extend those sheets, they'll never touch. That's the essence of parallel planes. They share the same 'direction,' if you will. The mathematical way to put this 'direction' is to use something called a "normal vector." This vector is perpendicular (at a 90 degree angle) to the plane.
So, if two planes are parallel, their normal vectors are parallel (or anti-parallel, meaning they point in opposite directions but are still aligned). In simpler terms, if you draw a line straight up from one plane, and another line straight up from the other, those lines either point the exact same way, or in precisely opposite ways. That shared direction ensures they never converge. Its kind of romantic, in a geometrical way. Isnt that something?
Think of it like train tracks — perfectly aligned so the train can chug along without a bumpy derailment. Okay, maybe a slight stretch, but the principle is the same! The distance between the track sections, similar to the space between our parallel planes, remains consistent and never allows any collision.
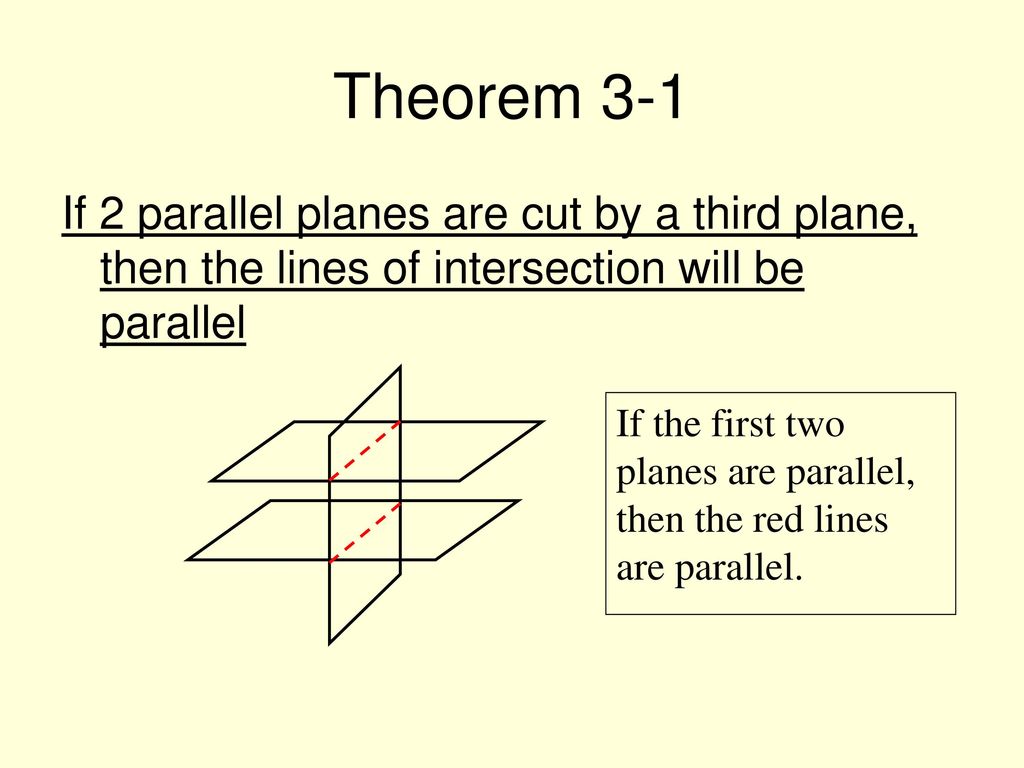
Parallel Lines Section Ppt Download
The Role of Normal Vectors
2. Decoding the Direction of a Plane
Normal vectors: those trusty arrows pointing directly out of a plane. They're our secret weapon in figuring out parallelism. Finding a normal vector might sound intimidating, but often its lurking within the equation of the plane itself. The equation of a plane is usually written in the form Ax + By + Cz + D = 0, where A, B, and C are constants. Guess what? The vector (A, B, C) is a normal vector to the plane! How handy is that?
Now, suppose you have two planes. Let's say the first plane has a normal vector n1, and the second plane has a normal vector n2. If n1 is a scalar multiple of n2, then the planes are parallel. What does that mean? It means you can get n1 by multiplying n2 by some number (a scalar). For example, if n1 = (2, 4, 6) and n2 = (1, 2, 3), then n1 = 2 n2, so the planes are parallel. Easy peasy, right?
However, if you're given two different normal vectors, you can also test for parallelism by seeing if they're linearly dependent. In layman's terms, this means you can't create one vector by simply scaling the other. If that's the case, the planes are going to intersect at some point, so they won't be parallel.
Imagine normal vectors as flags sticking out of our planes. If those flags are pointing in exactly the same or opposite directions, then the planes are parallel and will never meet. Thats how we can tell that these planes are in parallel harmony, dancing through geometrical space, never intersecting.
Checking for Parallelism: A Step-by-Step Guide
3. Putting Theory into Practice
Alright, let's get down to brass tacks (not nitty gritty!). Say you're confronted with two plane equations and you need to determine if they are parallel. Heres a simplified step-by-step guide:
- Identify the Normal Vectors: Pull out the coefficients from the x, y, and z terms in each plane equation. These coefficients form the normal vectors for each plane.
- Check for Scalar Multiples: See if one normal vector is a scalar multiple of the other. If it is, the planes are parallel! In other words, can you multiply all the components of one normal vector by the same number and get the other normal vector?
- Consider the Distance: Even if the normal vectors are parallel, make sure the planes aren't the same plane! A tricky situation. Check the constant 'D' in the plane equation. If, after normalizing the equations (making the coefficients in the normal vectors identical), 'D' is different, you've got parallel planes. If 'D' is the same, it's the same plane!
For instance, let's say we have planes defined by 2x + 4y + 6z + 1 = 0 and x + 2y + 3z + 5 = 0. The normal vectors are (2, 4, 6) and (1, 2, 3). Clearly, (2, 4, 6) = 2 (1, 2, 3), so the normal vectors are parallel. Because 1 and 5 are different constants and not scalar multiples of each other, the planes themselves are parallel.
Essentially, youre playing detective, looking for clues in the plane equations to unearth their relationship. By following these steps, you'll be a parallel plane-identifying pro in no time! It's like baking — follow the recipe, and you get the result you're looking for.
What if the Planes Aren't Parallel?
4. Exploring Intersecting Planes
So, what happens when the normal vectors aren't parallel? That means the planes will intersect. They are destined to meet, just not in a friendly, parallel way. When two planes intersect, they do so along a line. Imagine two pieces of cardboard slicing through each other — the intersection is where they meet and form a straight edge.
Finding the equation of that line of intersection can be a bit more involved, but it's doable. Usually involves solving a system of linear equations, and sometimes involves a bit of linear algebra sorcery. Basically, you're trying to find all the points that satisfy both plane equations simultaneously, which will give you the line of intersection.
Intersecting planes form angles with each other. The angle between the planes is actually the same as the angle between their normal vectors! So, if you find the angle between the normal vectors (using the dot product formula), you've found the angle between the planes. How neat is that?
Non-parallel planes dont just coexist politely; they carve out new geometrical spaces. They contribute to the complexity of the three-dimensional world around us, like architects creating intricate structures with careful intersections of planes. They are, in a way, the source of creativity in geometry.

2 Parallel Planes
Real-World Applications and FAQs
5. Parallel Planes in Everyday Life
You might be thinking, "Okay, parallel planes are neat and all, but where would I ever use this knowledge in the real world?" Well, buckle up, because parallel planes pop up in more places than you might think. Architecture uses the idea of parallel planes and normals every time buildings are designed, making sure the walls stay vertical (parallel to each other). Also, computer graphics employs parallel projections, which simulate parallel planes for creating 2D images of 3D objects.
Even something as simple as looking at a ruled notebook involves understanding parallel lines and planes. Each line you write on resides within a plane parallel to all the other lines on that page. Every book is built of flat planes stacked upon planes. In a way, a stack of books is very similar to a collection of parallel planes.
So, next time you're admiring a skyscraper or sketching out a design, remember the humble parallel plane and its role in creating the world around us. It might just give you a new appreciation for the geometrical harmony that underpins so much of our lives.
6. Frequently Asked Questions
Q: What if the coefficients A, B, and C in the plane equation are all zero?
A: That wouldn't be a plane! A, B, and C determine the normal vector, which gives the plane its orientation in space. If they're all zero, you don't have a plane equation anymore. You get D=0 (likely), which is less a plane, and more a mathematical identity.
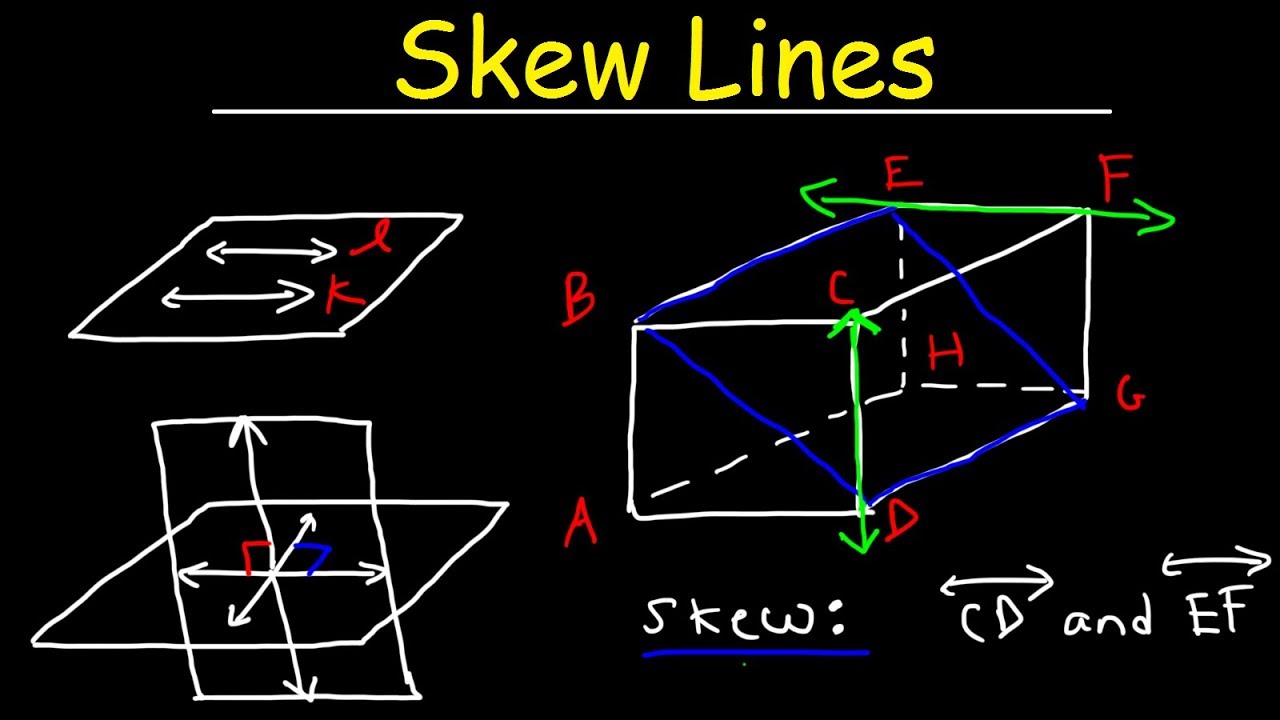
Q: Can parallel planes be "skew"?
A: No, skew is a term used for lines in 3D space that don't intersect and aren't parallel. Planes occupy an entire 2D space; therefore, they can't be "skew" relative to each other. They're either parallel or they intersect.
Q: Is there any relation between parallel lines and parallel planes?
A: Absolutely! A plane can contain an infinite number of parallel lines. And the condition for parallel planes ensures the lines they contain stay parallel to each other! They all hold hands together.

Lines & Planes Parallel, Perpendicular, And Skew Geometry Eat Pi
